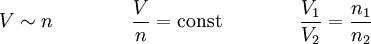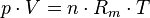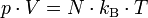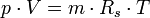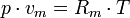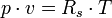Allgemeine Gasgleichung (Thermische Zustandsgleichung idealer Gase)

Die thermische Zustandsgleichung idealer Gase, oft auch vereinfacht und trivial als allgemeine Gasgleichung bezeichnet, beschreibt den Zusammenhang zwischen den thermischen Zustandsgrößen eines idealen Gases.
Sie vereint die experimentellen Einzelergebnisse und die hieraus abgeleiteten Gasgesetze zu einer allgemeingültigen Zustandsgleichung.
Viele Forscher und Wissenschaftler haben sich mit Gasen und ihrem Verhalten auseinandergesetzt und Teilergebnisse für die für uns gebräuchliche allgemeine Gasgleichung geliefert. Alle Teilwerke zusammengetragen, vereinen sich in der Formel
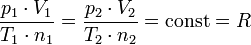
Gesetz von Boyle-Mariotte
Das Gesetz von Boyle-Mariotte (auch Boyle-Mariottesches Gesetz, Boyle-Mariotte-Gesetz oder Boyle’sches Gesetz) sagt aus,
dass der Druck idealer Gase bei gleichbleibender Temperatur (isotherme Zustandsänderung) und gleichbleibender Stoffmenge umgekehrt proportional zum Volumen ist.
Oder einfacher ausgedrückt:
Erhöht man den Druck auf Gas, wird durch den erhöhten Druck das Volumen verkleinert. Verringert man den Druck, so dehnt es sich aus.
Dieses Gesetz wurde unabhängig von zwei Physikern entdeckt, dem Iren Robert Boyle (1662) und dem Franzosen Edme Mariotte (1676).
Für T = konstant und n = konstant gilt:
Gesetz von Gay-Lussac
Das Gesetz von Gay-Lussac (auch 1. Gesetz von Gay-Lussac, Gay-Lussacsches Gesetz, Gesetz von Charles oder Charlessches Gesetz) besagt,
dass das Volumen idealer Gase bei gleichbleibendem Druck (isobare Zustandsänderung) und gleichbleibender Stoffmenge direkt proportional zur Temperatur ist.
Oder einfacher ausgedrückt:
Ein Gas dehnt sich bei einer Erwärmung aus und zieht sich bei einer Abkühlung zusammen.
Dieser Zusammenhang wurde 1787 von Jacques Charles und 1802 von Joseph Louis Gay-Lussac erkannt.
Für p = const und n = const gilt:
Das eigentliche Gesetz von Gay-Lussac (obiges ist nur der Teil, den man meist als das Gesetz von Charles bezeichnet) lautet aber:
Hierbei ist T0 die Temperatur am Nullpunkt der Celsiusskala, also 273,15 K oder 0 °C. Dagegen ist T die gesuchte Temperatur. Analog ist V das Volumen bei T, V0 das Volumen bei T0 und γ0 der Volumenausdehnungskoeffizient bei T0, wobei für ideale Gase allgemein γ = 1/T gilt.
Aus dieser Gleichung kann man nebenbei auch zusätzlich noch folgern, dass es einen absoluten Temperaturnullpunkt geben muss, da die Gleichung für diesen ein Volumen von Null voraussagt und das Volumen nicht negativ werden kann. Ihre empirische Basis ist daher auch Grundlage für die absolute Temperaturskala Kelvins, da hierüber durch Extrapolation der Temperaturnullpunkt bestimmt werden konnte.
Gesetz von Amontons
Das Gesetz von Amontons, (auch 2. Gesetz von Gay-Lussac), sagt aus,
dass der Druck idealer Gase bei gleichbleibendem Volumen (isochore Zustandsänderung) und gleichbleibender Stoffmenge direkt proportional zur Temperatur ist.
Oder wieder einfach gesagt:
Bei einer Erwärmung des Gases erhöht sich also der Druck und bei einer Abkühlung wird er geringer.
Dieser Zusammenhang wurde von Guillaume Amontons entdeckt.
Für V = const und n = const gilt:
Analog zum Gesetz von Gay-Lussac gilt hierbei auch:
Gesetz der Gleichförmigkeit
Das Gesetz der Homogenität sagt aus,
dass ein ideales Gas durch und durch homogen, das heißt gleichförmig, ist, dass es also überall dieselbe Dichte hat.
Wenn in einem großen Behälter mit einem homogenen Stoff, zum Beispiel mit einem Gas, an einer Stelle eine Teilmenge V1 eingeschlossen wird, so enthält diese dieselbe Stoffmenge wie eine Teilmenge mit demselben Volumen V1 an anderer Stelle. Teilt man die gesamte Stoffmenge auf zwei gleich große Volumina auf, so enthalten sie die gleiche Stoffmenge, nämlich die Hälfte der ursprünglichen. Daraus folgt:
Das Volumen ist bei gleichbleibendem Druck und gleichbleibender Temperatur proportional zur Stoffmenge.
Für T = const und p = const gilt:
Diese Gesetze gelten für alle homogenen Stoffe, solange Temperatur und Druck unverändert bleiben, und eben auch für ideale Gase.
Gesetz von Avogadro
Das Gesetz von Avogadro sagt aus,
dass zwei gleich große Gasvolumina, die unter demselben Druck stehen und die dieselbe Temperatur haben, auch dieselbe Teilchenzahl einschließen.
Dies gilt sogar dann, wenn die Volumina verschiedene Gase enthalten.
Selbstverständlich gilt es auch für den Fall, dass die Zusammensetzung in den beiden Volumina gleich ist; deswegen folgt auch aus dem Gesetz von Avogadro die Beziehung V ~ n für T = const und p = const. Darüber hinaus bedeutet es aber auch, dass ein Gas in einem bestimmten Volumen auch eine bestimmte Anzahl von Teilchen hat, die unabhängig von der Stoffart ist. Allerdings gibt es gewisse Ausnahmen, wenn zum Beispiel weniger oder zu viele Teilchen in einem Gaspaket sind.
Das Gesetz von Avogadro wurde 1811 durch Amedeo Avogadro entdeckt.
Es kann auch so formuliert werden:
Das molare Volumen ist bei einer bestimmten Temperatur und bei einem bestimmten Druck für alle idealen Gase identisch.
Messungen haben ergeben, dass ein Mol eines idealen Gases bei 0 °C = 273,15 K und 1013,25 hPa Druck ein Volumen von rund 22,4 dm³ einnimmt.
Eine bedeutende Folge dieses Gesetzes ist: Die Gaskonstante ist für alle idealen Gase identisch.
Die thermische Zustandsgleichung
Die Gleichung beschreibt den Zustand des idealen Gases bezüglich der Zustandsgrößen Druck p, Volumen V, Temperatur T und Stoffmenge n bzw. Teilchenzahl N bzw. Masse m. Sie kann in verschiedenen zueinander äquivalenten Formen dargestellt werden, wobei alle diese Formen den Zustand des betrachteten Systems in gleicher Weise und eindeutig beschreiben.
Ihre erste Formulierung stammt von Émile Clapeyron im Jahr 1834.
Extensive Formen:
Intensive Formen:
Hierbei stehen die einzelnen Formelzeichen für folgende Größen:
- kB – Boltzmann-Konstante
- m – Masse
- M – Molare Masse
- N – Teilchenzahl
- n – Stoffmenge
- p – Druck
- Rm – universelle oder molare Gaskonstante
- Rs – individuelle oder spezielle Gaskonstante
- ρ – Dichte
- T – absolute Temperatur
- vm – molares Volumen
- v – spezifisches Volumen
- V – Volumen
Die Gleichung stellt den Grenzfall aller thermischen Zustandsgleichungen für verschwindende Dichte 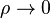 dar, das heißt für verschwindenden Druck bei genügend hoher Temperatur. In diesem Fall kann man das Eigenvolumen der Gasmoleküle und die Kohäsion – die anziehende Kraft zwischen den Molekülen – vernachlässigen. Die Gleichung ist für viele Gase wie zum Beispiel wasserdampfungesättigte Luft auch bei Normalbedingungen eine gute Näherung.
dar, das heißt für verschwindenden Druck bei genügend hoher Temperatur. In diesem Fall kann man das Eigenvolumen der Gasmoleküle und die Kohäsion – die anziehende Kraft zwischen den Molekülen – vernachlässigen. Die Gleichung ist für viele Gase wie zum Beispiel wasserdampfungesättigte Luft auch bei Normalbedingungen eine gute Näherung.
1873 erweiterte Johannes Diderik van der Waals das Gasgesetz zur Van-der-Waals-Gleichung, die das Eigenvolumen der Gasteilchen und die Anziehung zwischen ihnen im Gegensatz zur allgemeinen Gasgleichung mit berücksichtigt und somit auch als Näherung auf deutlich reale Gase angewendet werden kann. Eine andere Näherungslösung für reale Gase stellt die Reihenentwicklung der Virialgleichungen dar, wobei die allgemeine Gasgleichung identisch mit einem Abbruch der Reihenentwicklung nach dem ersten Glied ist.
Generell gilt, dass die allgemeine Gasgleichung als Näherungslösung für schwach reale Gase bei geringen intermolekularen Wechselwirkungen, kleinen Drücken und hohen Temperaturen (großen Molvolumina) geeignet ist. Insbesondere weisen ideale Gase hierbei keinen Joule-Thomson-Effekt auf.
Spezialfälle
Es gibt verschiedene Spezialfälle des allgemeinen Gasgesetzes, die einen Zusammenhang zwischen zwei Größen herstellen, während alle anderen Größen konstant gehalten werden.
Erklärt und nicht nur empirisch abgeleitet werden diese Zusammenhänge zwischen den Zustandsgrößen eines Gases durch dessen Teilchencharakter, also durch die kinetische Gastheorie.
Die kleinste Bewegung ist für die ganze Natur von Bedeutung!
Blaise Pascal
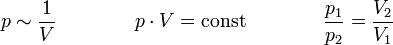
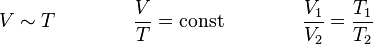
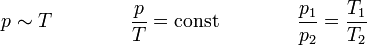
![p(T) = p_0 \left(1 + \gamma_0 [T - T_0]\right) \!](http://upload.wikimedia.org/math/4/9/3/4935808e112b4a9acee4bbeb5218fa9d.png)